티스토리 뷰

Algorithm 공부 #02 - 자료구조(배열과 리스트, 벡터와 구간 합)
배열
● 메모리의 연속 공간에 값이 채워져 있는 형태의 자료구조
● 인덱스를 사용하여 값에 바로 접근할 수 있음
● 배열의 크기는 선언할 때 저장할 수 있으며, 한 번 선언하면 크기를 늘리거나 줄일 수 없음
● 새로운 값을 삽입하거나 특정 인덱스에 있는 값을 삭제하기 어려움, 값을 삽입하거나
삭제하려면 해당 인덱스 주변에 있는 값을 이동시키는 과정이 필요함
● 구조가 간단하여 코테에서 많이 사용한다!
리스트
● 값과 포인터를 묶은 노드라는 것을 포인터로 연결하는 자료구조
● 인덱스가 없어서 값에 접근하기 위해 Head포인터부터 순서대로 접근해야 함, 값에 접근하는 속도가 느림
● 포인터로 연결되어 있어 데이터를 삽입하거나 연산하는 속도가 빠름
● 선언할 때 크기를 별도로 지정하지 않아도 됨, 리스트의 크기는 정해져 있지 않으며,
크기가 변하기 쉬운 데이터를 다룰 때 적절함
● 포인터를 저장할 공간이 필요하므로 배열보다 구조가 복잡함
벡터
● C++ 표준 라이브러리에 있는 자로구조 컨테이너 중 하나로, 사용자가 손쉽게 사용하기 위해 정의된 클래스
● 동적으로 원소를 추가할 수 있다, 즉 크기가 자동으로 늘어남
● 배열과 마찬가지로 인덱스를 사용하여 각 데이터에 직접적으로 접근할 수 있음
● 맨 마지막 위치에 데이터를 삽입하거나 삭제할 때는 문제가 없지만 중간 데이터의 삽입 삭제는
배열과 같은 메커니즘으로 동작함
※ Vector에 대해 더 자세히 알아보기 -> https://pooreumjung.tistory.com/2
#01 Vector
C++을 사용하는데 있어서 알면 너무나도 편리한 STL(Standard Template Library) Vector란?C++에는 두 가지 유형의 container가 있습니다. 그 중 Vector는 Sequence Container범주에 속합니다. 동적으로 메모리 할당이
pooreumjung.tistory.com
백준11720번 숫자의 합
https://www.acmicpc.net/problem/11720
11720번: 숫자의 합
첫째 줄에 숫자의 개수 N (1 ≤ N ≤ 100)이 주어진다. 둘째 줄에 숫자 N개가 공백없이 주어진다.
www.acmicpc.net

※ N의 범위가 1부터 100까지이므로 자료형 사용에 주의하기 -> 문자형으로 입력받고 숫자형으로 변환하기 ※
1. 숫자의 개수만큼 입력받은 값을 string형으로 저장하기
2. string형으로 입력받은 값을 한 칸씩 나누어서 char[]형으로 변환
3. 인데스 0부터 끝까지 배열을 탐색하여 각 값을 정수형으로 변환하고 결괏값에 누적하기
#include<iostream>
using namespace std;
int main() {
int N=0;
string numbers;
cin >> N;
cin>>numbers;
int sum = 0;
for (int i = 0; i < numbers.length(); i++) {
sum += numbers[i] - '0'; // numbers[i]를 정수로 계산하여 sum에 누적하기
}
cout << sum;
}
백준 1546번 평균 구하기
https://www.acmicpc.net/problem/1546
1546번: 평균
첫째 줄에 시험 본 과목의 개수 N이 주어진다. 이 값은 1000보다 작거나 같다. 둘째 줄에 세준이의 현재 성적이 주어진다. 이 값은 100보다 작거나 같은 음이 아닌 정수이고, 적어도 하나의 값은 0보
www.acmicpc.net
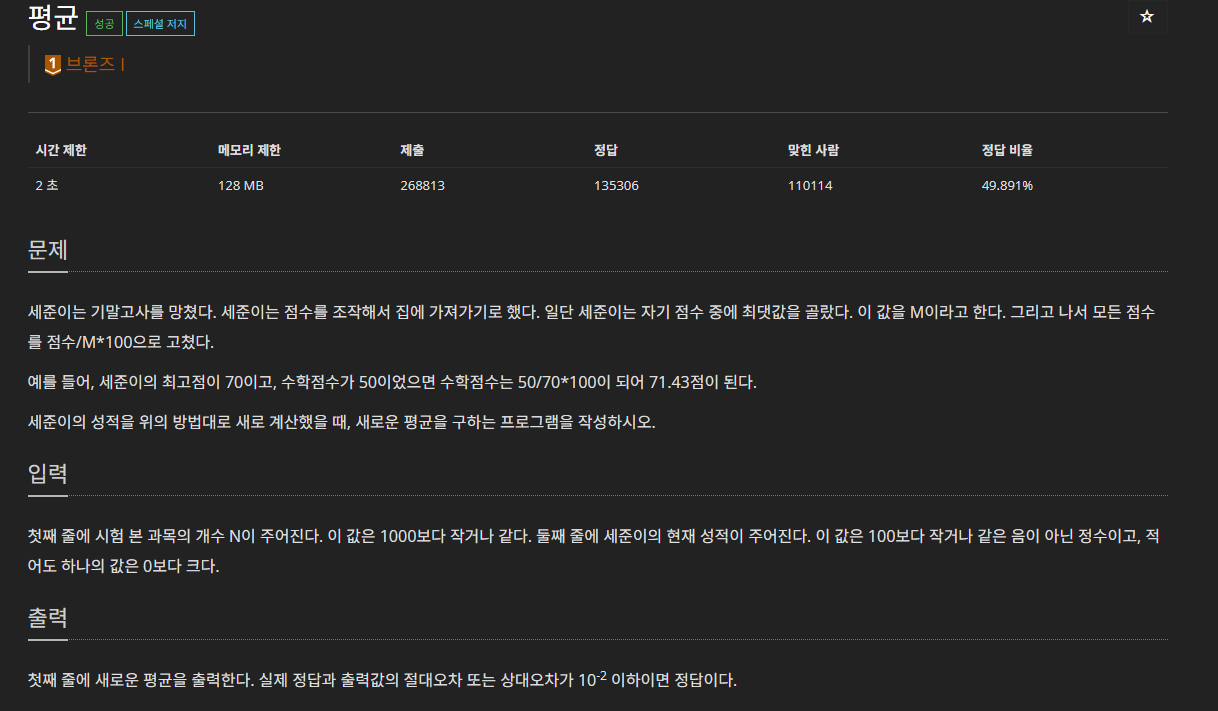


※ 모든 점수를 입력받은 후 최고점을 지정, 일일이 변환 점수를 구할 필요 없이 한 번에 변환한 점수의 평균 점수 구하기 ※
1. 점수를 1차원 배열에 저장
2. 배열을 탐색하여 최고 점수와 점수의 총합 구하기
3. 총합*100/ 최고 점수/ 과목의 수를 계산해 다시 계산하여 점수의 평균값 출력
#include<iostream>
using namespace std;
int main() {
int N = 0;
int A[1000];
cin >> N;
long sum = 0;
long max = 0;
for (int i = 0; i < N; i++) {
cin >> A[i];
if (max < A[i])
max = A[i];
sum += A[i];
}
double result = (sum * 100.0) / max / N;
cout << result;
}
구간 합
● 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘
● 합 배열을 구하는 공식 -> S[i] = S[i-1] + A[i]
● 구간 합을 구하는 공식 -> S[j] - S[i-1](i부터 j까지의 구간 합)
예제
백준 11659번 구간 합 구하기4
https://www.acmicpc.net/problem/11659
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
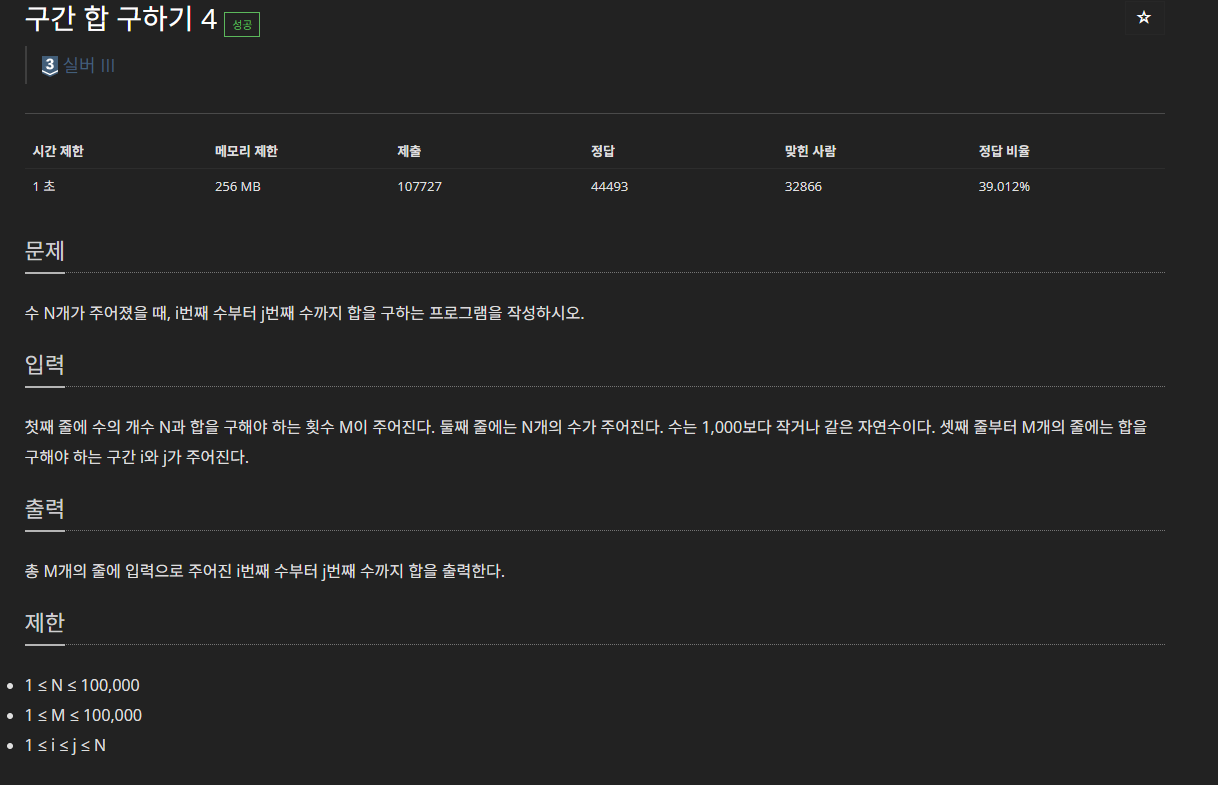

※ 문제에서 수의 개수와 합을 구해야 하는 횟수는 최대 100,000개, 구간마다 합을 매번 계산하면 1초안에 모든 구간 합
계산을 끝낼 수 없으므로 구간 합을 이용하기 ※
1. N개의 수를 입력받음과 동시에 합 배열을 생성하기
2. 구간 i~j가 주어지면 구간 합을 구하는 공식으로 정답 출력하기
#include<iostream>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
int sum[100001] = { 0 };
cin >> N >> M;
for (int i = 1; i <= N; i++) {
int temp;
cin >> temp;
sum[i] = sum[i - 1] + temp; //합 배열 만들기
}
for (int x = 0; x < M; x++) {
int i, j;
cin >> i >> j;
cout << sum[j] - sum[i - 1] << "\n"; // 구간 합 구하기
}
}
★ 위 코드에서 사용하였던 cin.tie(NULL)과 cout.tie(NULL)은 수행 속도가 빨라지는 효과를 만들어준다
cin과 cout은 기본적으로 하나로 묶여 있는데, 이것은 한 스트림이 다른 스트림에서 각 IO작업을 진행하기
전 자동으로 버퍼를 비워주는 것을 보장합니다. 특히 cin을 수행하기 전 기본적으로 cout 출력 버퍼를 지우는
작업을 수행하는데, 이 작업을 생략하기 때문에 속도가 빨라지는 효과기 있음(코테에서 유용함)
백준 11660번 구간 합 구하기5
https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
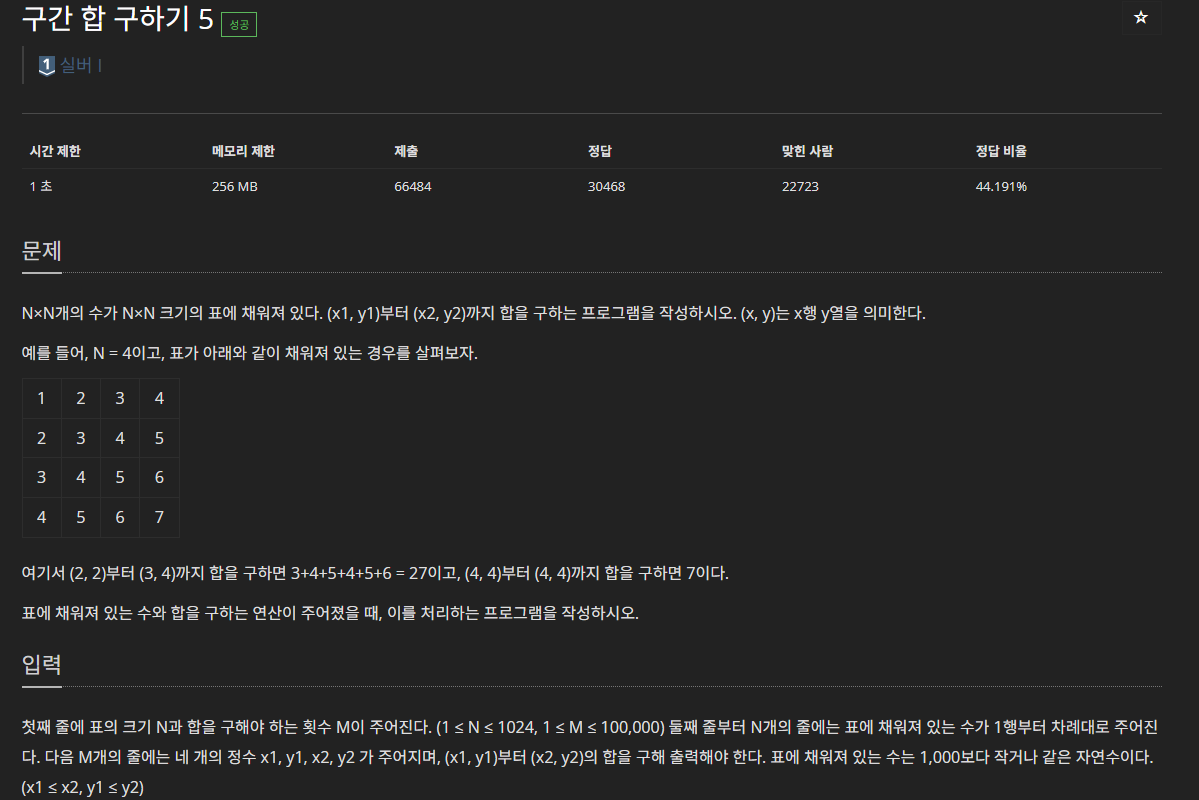
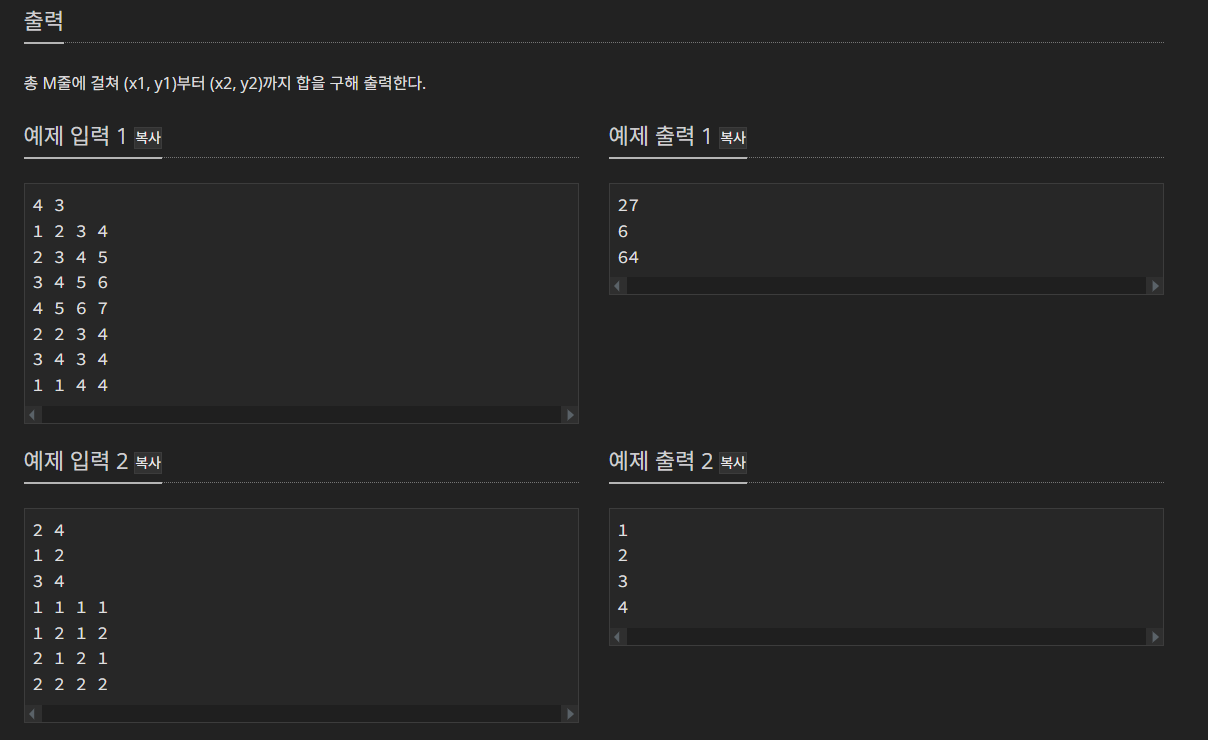
※ 질의의 개수가 100,000개이므로 질의마다 합을 구하면 안 되고, 구간 합 배열을 이용해야 함. 2차원 구간 합 배열을
사용하기
배열의 (0,0)부터 (i,j)까지의 사각형 영역 안에 있는 수의 합을 D[i][i]라고 할 때
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
배열의 구간 (X1,Y1)부터 (X2,Y2)의 합 구하기
D[X2][Y2] - D[X1-1][Y2] - D[X2][Y1-1] + D[X1-1][Y1-1] ※
#include<iostream>
using namespace std;
int A[1025][1025] = { 0 }; //지역변수로 두게 되면 메모리가 너무 커져서 실행 불가므로 전역변수로 설정
int D[1025][1025] = { 0 };
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
cin >> N >> M;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cin >> A[i][j];
D[i][j] = D[i - 1][j] + D[i][j - 1] - D[i - 1][j - 1] + A[i][j]; // 합 이차원 배열 구하기
}
}
for (int x = 0; x < M; x++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
int result = D[x2][y2] - D[x1 - 1][y2] - D[x2][y1 - 1] + D[x1 - 1][y1 - 1]; // 구간 합 구해주기
cout << result << "\n";
}
}
백준 10986번 구간 합 구하기5
https://www.acmicpc.net/problem/10986
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net

※ (A+b) % C는 ((A%C) + (B%C))와 같다. 다시 말해 특정 구간 수들의
나머지 연산을 더해 나머지 연산을 한 값과 이 구간 합의 나머지 연산을 한 값은 동일함
S[j] %M의 값과 S[i] %M의 값이 같다면 (S[j]-S[i]) % M은 0이다. 즉, 구간 합 배열의 원소를 M으로 나눈 나머지로
업데이트하고 S[i]와 S[j]가 같은 (i,j,)쌍을 찾으면 원본 배열에서 i+1부터 j까지의 구간 합이 M으로 나누어 떨어짐 ※
1. 배열 A의 합 배열 S를 생성하기
2. 합 배열 S의 모든 값을 M으로 나머지 연산을 수행해 값을 업데이트 하기
3. 변경된 합 배열에서 원소 값이 0인 개수만 세어 정답에 더하기
4. 변경된 합 배열에서 원소 값이 같은 인덱스의 개수를 세고 2개의 원소를 뽑는 모든 경우의 수를 구하여 정답에 더하기
#include<iostream>
#include<vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
cin >> N >> M;
vector<long> S(N, 0); //배열 생성
vector<long> C(M, 0);
long count = 0;
cin >> S[0];
for (int i = 1; i < N; i++) {
int temp;
cin >> temp;
S[i] = S[i - 1] + temp; // 합 배열 만들기
}
for (int i = 0; i < N; i++) {
int remainder = S[i] % M;
if (remainder == 0) // 나머지 연산을 했을 때 나누어 떨어지므로 정답에 더하기
count++;
C[remainder]++;
}
for (int i = 0; i < M; i++) {
if (C[i] > 1) // 나머지 연산 후 0이 아닌 원소들에 한하여 2개의 원소를 뽑는 모든 경우의 수를 구하기
count = count + (C[i] * (C[i] - 1) / 2);
}
cout << count;
}
'Algorithm > 알고리즘 공부 일기' 카테고리의 다른 글
| Algorithm 공부 #06 - 정렬(삽입 정렬과 퀵 정렬) (2) | 2024.03.01 |
|---|---|
| Algorithm 공부 #05 - 정렬(버블 정렬과 선택 정렬) (0) | 2024.02.29 |
| Algorithm 공부 #04 - 자료구조(스택과 큐) (0) | 2024.02.28 |
| Algorithm 공부 #03 - 자료구조(투 포인터와 슬라이딩 윈도우) (2) | 2024.02.27 |
| Algorithm 공부 #01 - 시간 복잡도와 디버깅 (2) | 2024.02.24 |
- Total
- Today
- Yesterday
- java
- html
- DFS
- 백준 풀이
- 자바
- 스택
- C++
- 투 포인터
- BFS
- c++ string
- C++ Stack
- 반복문
- CSS
- Do it!
- HTML5
- 유클리드 호제법
- 유니온 파인드
- 스프링 부트 crud 게시판 구현
- 세그먼트 트리
- 카운팅 정렬
- 자료구조
- 이분 매칭
- js
- 에라토스테네스의 체
- 우선순위 큐
- 알고리즘
- 알고리즘 공부
- 자바스크립트
- DP
- 백준
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
