티스토리 뷰
Algorithm 공부 #22 - 최소 공통 조상(Lowest Common Ancestor)
최소 공통 조상(lowest common ancestor)
● 최소 공통 조상 : 임의의 두 노드를 선택 후, 두 노드가 각각 자신을 포함해 거슬러 올라가면서
부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드
● 선택된 누 노드의 깊이가 다른 경우: 더 깊은 노드를 부모 노드로 1개씩 올려 주면서 깊이를 맞춰줌
이때, 두 노드가 같다면 해당 노드가 최소 공통 조상이므로 탐색 종료
최소 공통 조상 빠르게 구하기
● 서로의 깊이를 맞춰 주거나 같아지는 노드를 찾을 때 기존에는 한 단계씩 올려 주는 방식이었다면
이 방식은 2^k씩 올라가면서 맞춰주는 방식
● 기존에 자신의 부모 노드만 저장해 놓던 방식에서 2^k번째 위치의 부모 노드까지 저장
● 구현 방법
1. 부모 노드 저장 배열 만들기
P[K][N] = N번 노드의 2^K번재 부모의 노드 번호
P[K][N] = P[K-1][[P[K-1][N]]
여기서 K는 트리의 깊이 > 2^K를 만족하는 K의 최댓값
2. 선택된 두 노드의 깊이 맞추기
P배열을 이용해 기존에 한 단계씩 맞췄던 깊이를 2^K 단위로 넘어가면서 맞추기
만약 높이 차이가 20이라고 가정하면 2^K<=20을 만족하면서 K가 최대가 되는 만큼 이동하면서
높이 차이가 0이 될 때까지 이동 => 2^4(16 )-> 2^2(4)와 같이 두 번 이동
3. 최소 공통 조상 찾기
2^K단위로 점프하면서 맞추면서 최초로 두 노드의 부모가 달라지는 값 찾기
이 두 노드의 값이 같다면 이 노드가 최소 공통 조상이고, 다르다면 바로 위의 부모 노드가 최소 공통 조상
백준 11437번 LCA
https://www.acmicpc.net/problem/11437
11437번: LCA
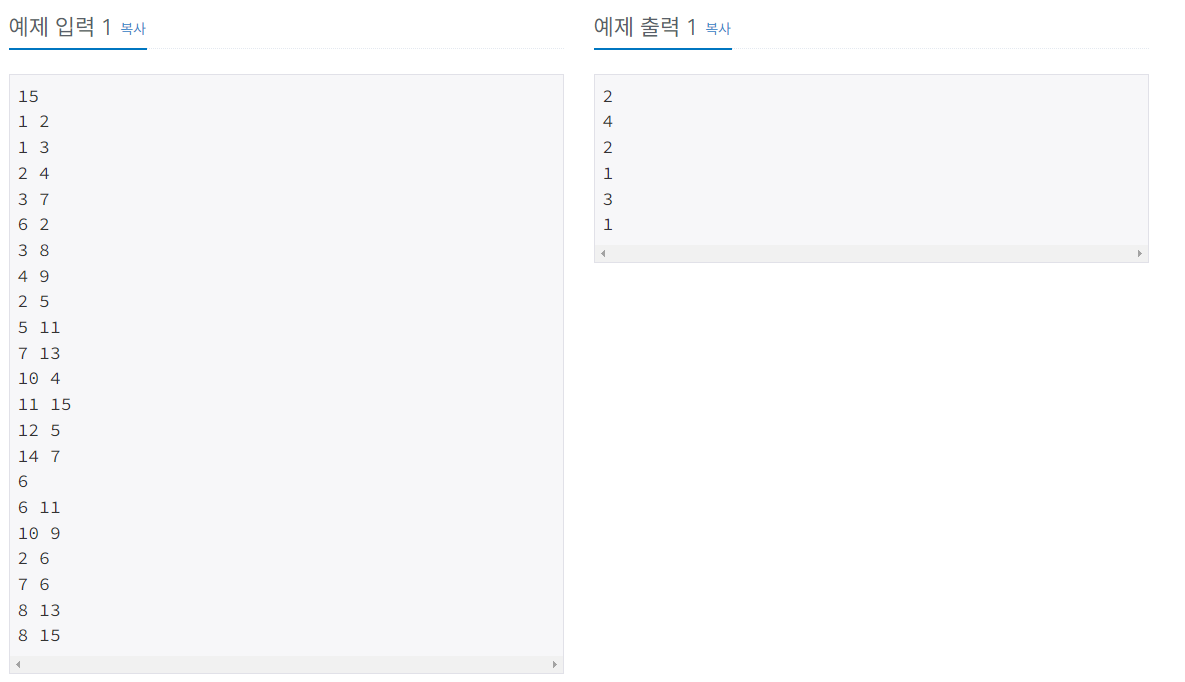
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net

● 인접 리스트로 그래프 구현
● bfs로 그래프를 탐색하며 각 노드들의 부모 노드와 깊이를 갱신
● executeLCA함수로 최소 공통 조상 찾아주기
1. start의 깊이를 더 깊게 만들어주기
2. 두 노드의 깊이를 맞춰주기, start의 깊이가 더 깊으므로 start의 값을 계속 start의 부모 노드 값으로 갱신해주기
3. 두 노드의 깊이를 맞춰주었다면, 같은 조상이 나올 때까지 한 칸씩 더 돌리기(start==end라면 안해줘도 됨)
백준 11438번 LCA2
https://www.acmicpc.net/problem/11438
11438번: LCA 2
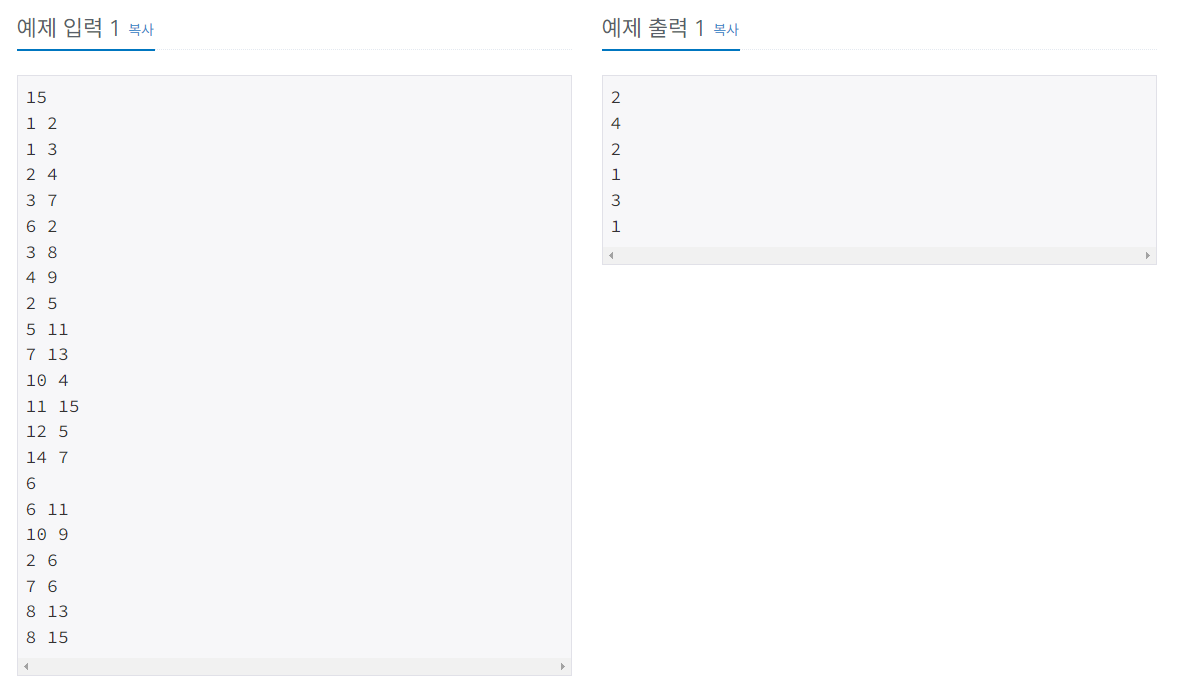
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net

● N의 값이 크기 때문에 제곱수 형태를 이용한 빠르게 최소 공통 조상 구하기 방식으로 접근
● 부모 노드를 2^k형태로 저장하기 / bfs탐색시에는 모든 노드의 깊이와 2^0번째 부모노드를 저장
● 그 후에 for문을 돌리면서 각 노드의 2^k부모 노드까지 저장
● executeLCA함수에서 깊이를 맞춰주고 조상을 찾아줌
#include <iostream>
#include <vector>
#include <queue>
#include<cmath>
using namespace std;
static int N, M;
static vector < vector <int> > tree;
static vector<int> depth;
static int kmax;
static int parent[21][100001];
static vector<bool> visited;
int excuteLCA(int a, int b);
void BFS(int node);
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
tree.resize(N + 1);
for (int i = 0; i < N - 1; i++) { // A인접리스트에 그래프 데이터 저장
int s, e;
cin >> s >> e;
tree[s].push_back(e);
tree[e].push_back(s);
}
depth.resize(N + 1);
visited.resize(N + 1);
int temp = 1;
kmax = 0;
while (temp <= N) { // 최대 가능 Depth 구하기
temp <<= 1;
kmax++;
}
BFS(1); // depth를 BFS를 통하여 구하기
for (int k = 1; k <= kmax; k++) { // 점화식을 이용한 parent 배열 채우기
for (int n = 1; n <= N; n++) {
parent[k][n] = parent[k - 1][parent[k - 1][n]];
}
}
cin >> M;
for (int i = 0; i < M; i++) {
// 공통 조상을 구할 두 노드
int a, b;
cin >> a >> b;
int LCA = excuteLCA(a, b);
cout << LCA << "\n";
}
}
int excuteLCA(int a, int b) {
if (depth[a] > depth[b]) {//더 깊이가 깊은 depth가 b가 되도록 변경해주기
int temp = a;
a = b;
b = temp;
}
for (int k = kmax; k >= 0; k--) {// depth 빠르게 맞춰주기
if (pow(2, k) <= depth[b] - depth[a]) {
if (depth[a] <= depth[parent[k][b]]) {
b = parent[k][b];
}
}
}
for (int k = kmax; k >= 0 && a != b; k--) { // 조상 빠르게 찾기
if (parent[k][a] != parent[k][b]) {
a = parent[k][a];
b = parent[k][b];
}
}
int LCA = a;
if (a != b)
LCA = parent[0][LCA];
return LCA;
}
// BFS구현
void BFS(int node) {
queue<int> myqueue;
myqueue.push(node);
visited[node] = true;
int level = 1;
int now_size = 1;
int count = 0;
while (!myqueue.empty()) {
int now_node = myqueue.front();
myqueue.pop();
for (int next : tree[now_node]) {
if (!visited[next]) {
visited[next] = true;
myqueue.push(next);
parent[0][next] = now_node; // 부모 노드 저장
depth[next] = level; //노드 depth 저장
}
}
count++;
if (count == now_size) {
count = 0;
now_size = myqueue.size();
level++;
}
}
}
'Algorithm > 알고리즘 공부 일기' 카테고리의 다른 글
| Algorithm 공부 #24 - dp(동적 계획법) (0) | 2024.03.22 |
|---|---|
| Algorithm 공부 #23 - 조합(combination) (0) | 2024.03.18 |
| Algorithm 공부 #21 - 세그먼트 트리 (0) | 2024.03.16 |
| Algorithm 공부 #20 - 이진 트리(Binary Tree) (0) | 2024.03.16 |
| Algorithm 공부 #19 - 트리의 특성과 트라이 (0) | 2024.03.15 |
- Total
- Today
- Yesterday
- 이분 매칭
- 유클리드 호제법
- DFS
- c++ string
- 자바
- DP
- 스택
- 에라토스테네스의 체
- java
- 카운팅 정렬
- js
- 자바스크립트
- 반복문
- Do it!
- 투 포인터
- html
- HTML5
- C++
- 우선순위 큐
- 백준
- 자료구조
- BFS
- 스프링 부트 crud 게시판 구현
- 알고리즘
- 알고리즘 공부
- 백준 풀이
- CSS
- 유니온 파인드
- 세그먼트 트리
- C++ Stack
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
