티스토리 뷰

Algorithm 공부 #27 - KMP알고리즘
✏️ 단순 문자열 비교 알고리즘
말 그대로 단순히 for문을 돌리면서 문자열을 하나하나씩 비교하는 알고리즘
하지만 이렇게 돌리게 되면 두 문자열의 길이를 n과 m이라고 했을 때 시간복잡도가 O(n*m)이고 n과 m이 1,000,000이상만 넘어가도 많은 시간이 걸리게 되는 단점이 있음
먼저 긴 문자열을 parent(BCDEF)라 하고 찾을 문자열을 DE라고 하면
가장 먼저 찾을 문자열을 parent맨 앞에 위치시키고 비교 => 맞지 않음

다시 인덱스를 한 칸 뒤로 옮겨서 비교 => 맞지 않음

다시 인덱스를 한 칸 뒤로 옮겨서 비교 => 정답

이런 식으로 비교를 하게 되면 짧은 문자열은 상관이 없지만 문자열이 길어질수록 시간이 오래 걸리게 됨
✏️ KMP 알고리즘이란?
문자열을 매칭하는 알고리즘로써 대표적인 문자열 매칭 알고리즘
즉, 문자열들이 주어졌을 때 그 안에서 겹치는 문자열들을 찾아내주는 알고리즘
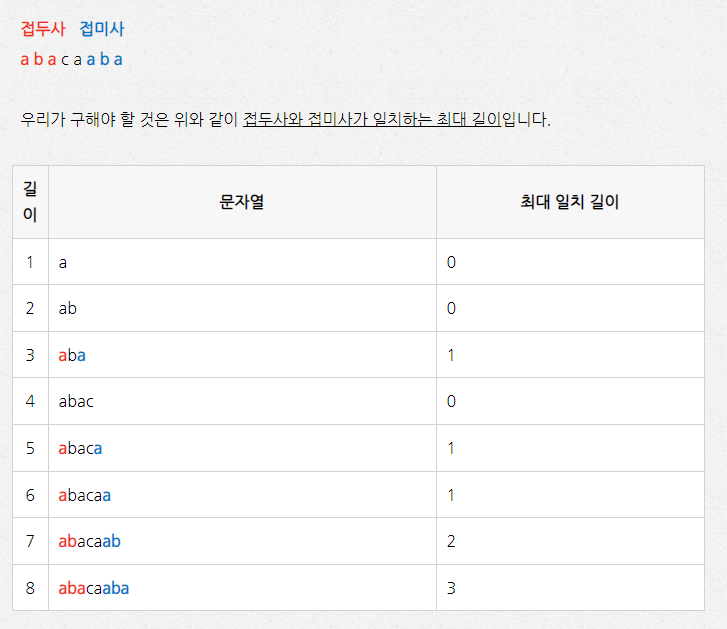
접미사와 접두사의 개념을 이용해서 점프하는 식으로 찾아냄
다음과 같은 문자열이 주어졌을 때 접두사와 접미사가 일치하는 최대 길이를 알아내야 함
이렇게 구해놓게 되면 나중에 접두사와 접미사가 일치하는 부분에서 점프를 할 수 있기 때문에 효율적임
이런 과정을 구하는 함수를 "실패 함수"를 구현한다고 함
✏️ 실패 함수
#include<iostream>
#include<vector>
#include<string>
using namespace std;
vector<int>makeFailTable(string pattern);
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
string pattern = "abacaaba";
vector<int>table = makeFailTable(pattern);
for (int i = 0; i < table.size(); i++)
cout << table[i] << " ";
}
vector<int> makeFailTable(string pattern)
{
int patternSize = pattern.size();
vector<int>table(patternSize, 0);
int j = 0;
for (int i = 1; i < patternSize; i++) {
while (j > 0 && pattern[i] != pattern[j])
j = table[j - 1];
if (pattern[i] == pattern[j])
table[i] = ++j;
}
return table;
}위와 같이 실패함수를 구현할 수 있음
방식을 설명해보자면, while문 안에서 i와 j를 어떻게 움직일 것인가?가 관건이 됨
일단 먼저 j=0으로 i=1로 두고 시작하기
j>0보다 큰 구간에서 pattern[i] != pattern[j]일 때는 접두사와 접미사가 일치하지 않는다고 생각하면 됨
그러면 j값을 table[j-1]로 변경을 시켜주기 => table배열에는 각 인덱스마다 일치하는 최대 길이를 저장하고 있는데 만약 어느 한 부분에서 일치하지 않는다면 바로 그 전 지점까지는 일치한다는 말이기 때문에 j = table[j-1]로 변경
차피 i는 for문 안에서 계속 증가하고 있기 때문에 신경쓰지 않아도 됨
이제 어느 순간에서는 pattern[i] == pattern[j]인 순간이 오게 됨
그러면 table[i]값을 ++j값으로 저장 => 위에서도 알 수 있지만 table배열은 각 인덱스마다 일치하는 최대 길이를 저장하고 있고 j값도 그에 따라서 같이 움직이고 있기 때문에 매 순간 j는 i-1까지의 최대 길이 정보를 저장하고 있음
거기서 문자열이 일치하면 문자 한 개가 더 추가로 일치하는 거기 때문에 table[i]에 ++j를 넣어서 두 개의 값을 동시에 변경
✏️ KMP함수
실패 함수를 구했으니, 이제는 문자열을 매칭해볼 차례
함수를 구현하기에 앞서 먼저 예시로 살펴보기
주어진 문자열을 "ababacabacaabacaaba"라 하고
찾을 문자열을 "abacaaba"라고 하면
이미 우리는 위에서 "abacaaba" 의 실패 함수를 구축했기 때문에 이를 이용해야 함
먼저 주어진 문자열과 찾을 문자열을 하나씩 비교하기
맨 첫 글자는 동일 => 다음거로 탐색

세 번째 글자까지 동일 => 계속 탐색

네 번째 글자 탐색 => 다르다
서로 다른 문자가 발견되면 일치하는 접두사 부분에 한해서만 부분 문자열의 인덱스를 이동시킴
즉 ab까지는 일치한다는 점을 이용한다는 말


시작점을 바꿔줬으니 다시 하나씩 탐색하기 => a로 같으니까 인덱스 증가

이렇게 증가시키다보면은 일치하는 순간이 나오게 됨
그리고 발견한 경우에도 접두사가 일치하는 한 가장 큰 길이만큼만 이동시키는 식으로
반복해서 매칭시키면 모든 문자열을 찾을 수 있음

#include<iostream>
#include<vector>
#include<string>
using namespace std;
vector<int>makeFailTable(string pattern);
void KMP(string parent, string pattern);
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
string pattern = "abacaaba";
string parent = "ababacabacaabacaaba";
KMP(parent, pattern);
}
vector<int> makeFailTable(string pattern)
{
int patternSize = pattern.size();
vector<int>table(patternSize, 0);
int j = 0;
for (int i = 1; i < patternSize; i++) {
while (j > 0 && pattern[i] != pattern[j])
j = table[j - 1];
if (pattern[i] == pattern[j])
table[i] = ++j;
}
return table;
}
void KMP(string parent, string pattern)
{
vector<int>table = makeFailTable(pattern);
int patternSize = pattern.size();
int parentSize = parent.size();
int j = 0;
for (int i = 0; i < parentSize; i++) {
while (j > 0 && parent[i] != pattern[j]) {
j = table[j - 1];
}
if (parent[i] == pattern[j]) {
if (j == patternSize - 1) {
cout << i - patternSize + 2 << "에서 일치함" << "\n";
j = table[j];
}
else
j++;
}
}
}
KMP함수도 실패 함수 구현과 그렇게 많이 다르지는 않음
우선 긴 문자열이 parent이므로 parent길이만큼 반복문을 돌리기
그 다음 while문 부분을 보면은 실패 함수 부분의 while문과 똑같음, 다만 비교하는 부분이 parent[i] 와 pattern[j]의 차이
parent[i] == pattern[j]라면 두 가지 경우로 나뉘게 됨
1. pattern의 문자열을 다 찾은 경우
i - patternSize +2부분에서 일치함 => 기본적으로 i-patternSize+1을 해줘야 하지만 배열의 인덱스를 0부터 시작했기 때 문에 1을 더 더해줘야 함, 그 후 j=table[j]로 업데이트, table배열은 일치하는 최대 길이를 저장하는 배열임을 생각해야 함
2. 다 찾지 못한 경우
j값을 증가시켜서 다음 인덱스로 넘어갈 수 있도록 해주기
✏️ KMP함수 기본 예제
https://pooreumjung.tistory.com/356
[C/C++] 백준 1786번 - 찾기
✏️문제 링크 https://www.acmicpc.net/problem/1786 1786번: 찾기 첫째 줄에, T 중간에 P가 몇 번 나타나는지를 나타내는 음이 아닌 정수를 출력한다. 둘째 줄에는 P가 나타나는 위치를 차례대로 공백으로
pooreumjung.tistory.com
사진 자료들은 안경잡이개발자 "동빈나"님의 블로그를 참고했습니다!
https://blog.naver.com/ndb796/221240660061
30. KMP(Knuth-Morris-Pratt) 알고리즘
이번 시간에 다루게 될 알고리즘은 KMP 알고리즘으로 대표적인 문자열(String) 매칭 알고리즘입...
blog.naver.com
'Algorithm > 알고리즘 공부 일기' 카테고리의 다른 글
| Algorithm 공부 #28 - 확장 유클리드 호제법(Extended Euclidean Algorithm) (0) | 2024.04.27 |
|---|---|
| Algorithm 공부 #26 - 이분 매칭(Binary Matching) (0) | 2024.04.14 |
| Algorithm 공부 #25 - 기하학(Geometry) (2) | 2024.03.30 |
| Algorithm 공부 #24 - dp(동적 계획법) (0) | 2024.03.22 |
| Algorithm 공부 #23 - 조합(combination) (0) | 2024.03.18 |
- Total
- Today
- Yesterday
- DP
- 에라토스테네스의 체
- 반복문
- C++
- DFS
- 카운팅 정렬
- 백준 풀이
- html
- 스택
- 자바스크립트
- 세그먼트 트리
- BFS
- CSS
- 유클리드 호제법
- 자료구조
- C++ Stack
- 이분 매칭
- 스프링 부트 crud 게시판 구현
- 유니온 파인드
- 알고리즘 공부
- 알고리즘
- js
- Do it!
- java
- 투 포인터
- 자바
- 백준
- c++ string
- HTML5
- 우선순위 큐
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
