티스토리 뷰
반응형
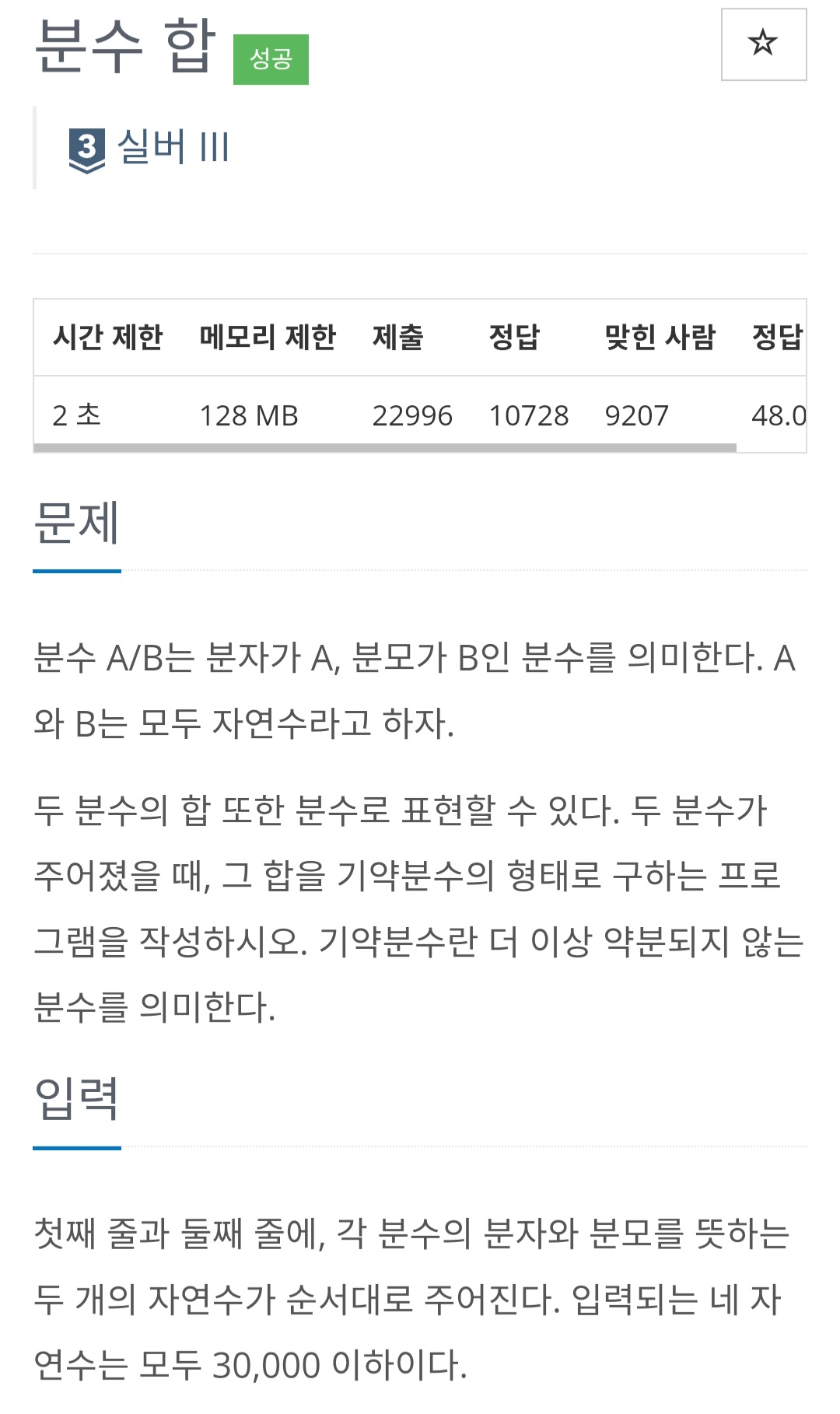
백준 1735번 분수 합
https://www.acmicpc.net/problem/1735
1735번: 분수 합
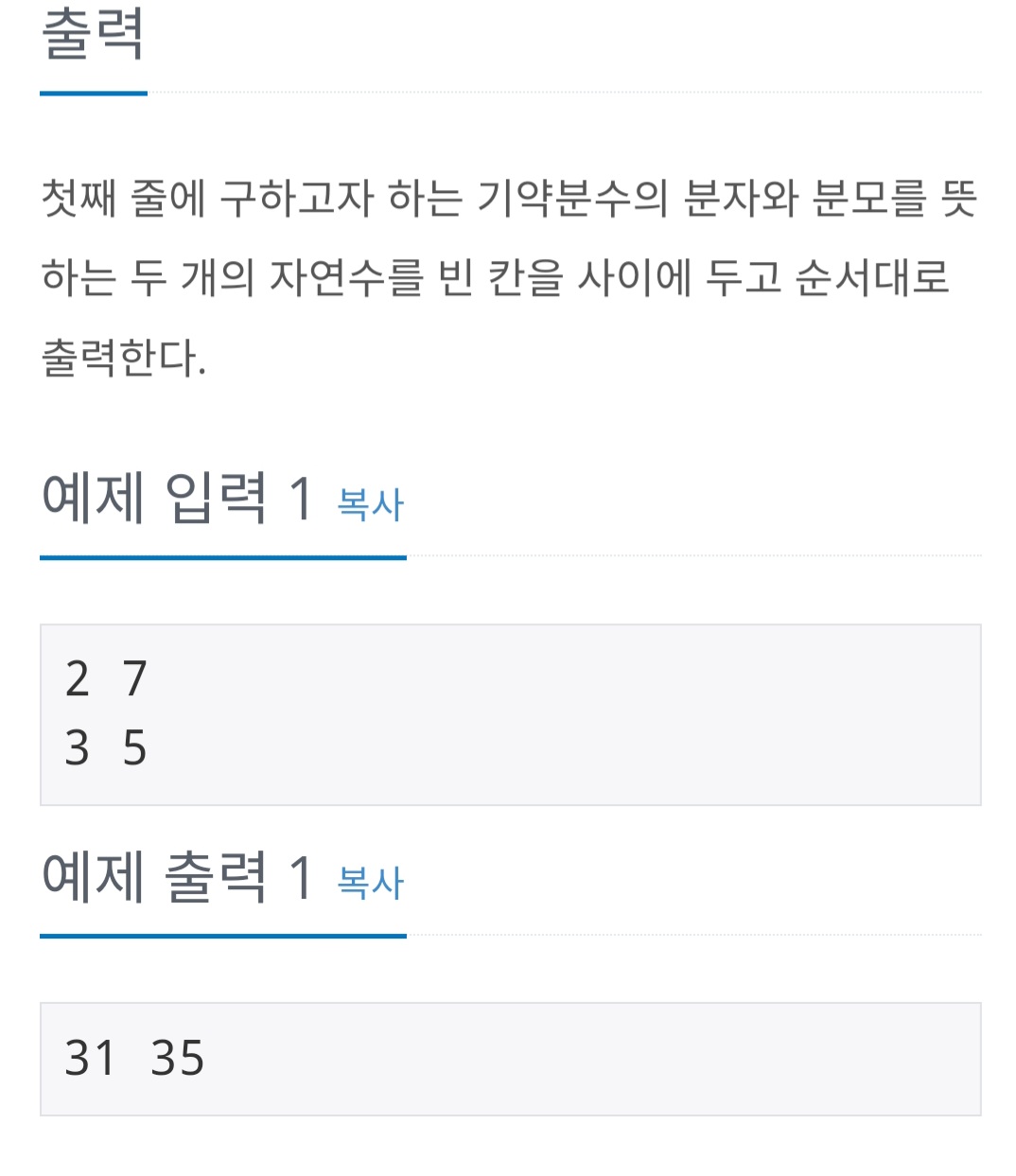
첫째 줄과 둘째 줄에, 각 분수의 분자와 분모를 뜻하는 두 개의 자연수가 순서대로 주어진다. 입력되는 네 자연수는 모두 30,000 이하이다.
www.acmicpc.net
정답 코드
#include <iostream>
#include <string>
using namespace std;
int GCD(int, int);
int main()
{
int numerator, denominator;
int numerator1, denominator1;
int numerator2, denominator2;
int gcd;
cin >> numerator1 >> denominator1;
cin >> numerator2 >> denominator2;
if (denominator1 == denominator2)
{
numerator = numerator1 + numerator2;
denominator = denominator1;
}
else
{
numerator = (numerator1 * denominator2) + (numerator2 * denominator1);
denominator = denominator1 * denominator2;
}
gcd = GCD(denominator, numerator);
cout << numerator / gcd <<" "<< denominator / gcd << endl;
return 0;
}
int GCD(int B, int A)
{
if (B % A == 0)
return A;
else
return GCD(A, B%A);
}
문제 풀이
기약분수에 관한 문제입니다. 이를 해결하기 위해서는
일반적인 분수 덧셈과정에서의 통분, 그리고 나서 최대공약수를 통한 약분을 하는 문제입니다. 다만 최대공약수를 구하기 위해서는 유클리드 호제법이라는 알고리즘을 사용해야 합니다.
유클리드 호제법이란 A=bq+r일때
GCD(A,B)=GCD(q,r)입니다.
G가 A와b의 약수라면 동시에 G는 A-B의 약수입니다.
또한 A를 b로 나눴을 때 나머지가 r이라면
A와 b의 최대공약수는 b와 r의 최대공약수입니다.
더 자세한 건 여기를 클릭해보세요
.
반응형
'Algorithm > BOJ' 카테고리의 다른 글
| 백준 1748번 C++ (0) | 2023.07.25 |
|---|---|
| 백준 1747번 C++ (0) | 2023.07.25 |
| 백준 1712번 C++ (0) | 2023.07.25 |
| 백준 1697번 C++ (0) | 2023.07.25 |
| 백준 1676번 C++ (0) | 2023.07.25 |
반응형
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 백준
- DP
- 자바
- 투 포인터
- c++ string
- BFS
- 반복문
- 이분 매칭
- 우선순위 큐
- js
- C++
- 자료구조
- CSS
- 스택
- 에라토스테네스의 체
- DFS
- html
- 알고리즘 공부
- 백준 풀이
- 알고리즘
- HTML5
- Do it!
- java
- 카운팅 정렬
- 유니온 파인드
- 스프링 부트 crud 게시판 구현
- 유클리드 호제법
- 세그먼트 트리
- C++ Stack
- 자바스크립트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
글 보관함
